
Studies of excited nuclear states by using the 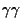 -
coincidence technique
-
coincidence technique
Lab Exercise in Nuclear Physics
In this lab exercise we will study the excited states of a nucleus
by the so-called coincidence technique using two germanium detectors.
The exercise aims to teach you to:
- Connect and tune the experimental equipment by yourself.
- Understand and be able to use some common signal processing devices.
- Understand the idea behind coincidence measurements.
- Build up a level scheme based on the measured coincidence data.
- Interpret the different structures of the level scheme.
Before the lab exercise you should read
the following chapters in the Krane
textbook (K.S. Krane, Introductory Nuclear Physics).
- Energy Measurements, (Krane, chapter 7.6)
- Coincidence Measurement, (Krane, chapter 7.7)
- Collective Structure, esp. Rotational Bands, (Krane, chapter 5.2)
To get a high quality printed version of this lab instruction
you can use the pdf
version.
Every quantum mechanical system can be described theoretically by its
Hamilton operator. From this operator, the eigenfunctions and
eigenvalues of the system can, at least in theory, be deduced. This
means that the nucleus is described by a model that can be checked
e.g. by experimentally measuring energy levels. In the course in
nuclear physics both the shell model and models for collective
motion are described. The validity of the models can of course also
be tested by measurement of other observables, for example the total
moment of inertia, the magnetic dipole moment, the electrical
quadrupole moment and the transition probabilities. These are related to
the wave functions of the nucleus through the matrix element for a
given operator. In order to further develop the theories of the
nucleus and to be able to understand new phenomena, it is thus
important to measure how the excited states of the nucleus are
distributed.
If we can create the nucleus in an excited state, for example using a
nuclear reaction or through alpha or beta decay, the nucleus is often
deexcited by the emission of a cascade of gamma radiation. This
cascade connects different states with each other. If we use only one
detector to detect the gamma decay we get a so-called singles
spectrum, from which it is not possible to deduce anything about the
relative positions of the energy levels. We only get a number of peaks in the
spectrum which correspond to the energy differences between different
states in the nucleus. In order to build up the level scheme, the
deexcitations of the nucleus must in some way be related to each
other. This can be done by using at least two gamma ray detectors in
the experimental setup, and demanding that these detect one gamma
quantum each during a time gate with a length that is comparable to
a typical life time of a nuclear state.
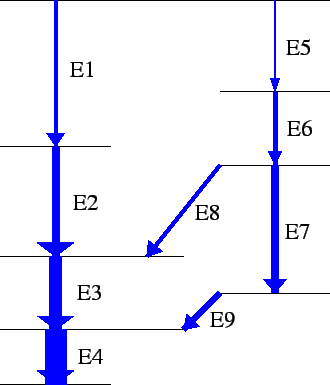
Figure 1:
Part of a level scheme. If we use only one detector to
count the decays from several nuclei in the source we obtain a so-called singles spectrum
where all the energies E1-E9 can be seen. But if we can count which 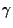 -photons
that were emitted in a cascade from one single nucleus we can obtain information
about the position of the levels in the level scheme.
-photons
that were emitted in a cascade from one single nucleus we can obtain information
about the position of the levels in the level scheme.
|
|
By systematically choosing each of the peaks that are in the singles
spectrum, and for each such peak look at what other transitions appear
in the same cascade as this peak, a number of conditions that will
have to be fulfilled in the final level scheme can be deduced. If
another nucleus happens to decay during the same time gate,
transitions may appear to be in coincidence although they are really
not. These events are called random coincidences and give an unwanted
background. The number of detected events that are of this kind
depends on the number of gamma rays that hit each detector per unit of
time. If the number of events in detectors 1 and 2 are 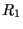 and
and 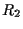 per second and the time gate is
per second and the time gate is 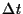 seconds wide, in average
seconds wide, in average
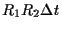 random coincidences are detected each second. By
minimizing the time gate, this number can be kept at an acceptable
level. In some cases a level is metastable, or isomeric, which has
as a consequence that all transitions that are below (or after) this
level will end up outside this time gate if the gate is started by a
transition above this level. In such a case, the levels below and above
the isomeric state can be tied together by increasing the length of
the time gate.
random coincidences are detected each second. By
minimizing the time gate, this number can be kept at an acceptable
level. In some cases a level is metastable, or isomeric, which has
as a consequence that all transitions that are below (or after) this
level will end up outside this time gate if the gate is started by a
transition above this level. In such a case, the levels below and above
the isomeric state can be tied together by increasing the length of
the time gate.
For the measurements, two Ge detectors made from highly enriched
germanium (Krane, ch 7.4) will be used. The detectors are kept in
contact with a container of liquid nitrogen through a cooling rod
made from copper. This reduces the thermal noise in the detectors,
caused by thermal excitations of electrons across the band gap, that
will otherwise disturb the measurements. The detectors also have a
temperature sensor. Through feedback of this signal to
the voltage supply, the detector will automatically shut down if the
temperature of the crystal becomes to high. This function is called
Bias Shutdown.
Figure 2:
A sketch of the experimental setup of the lab exercise. The
abbreviations and the functionality of the units are explained below.
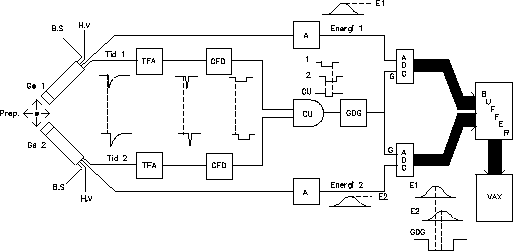 |
Two identical output signals are taken from each detector. After the
pre-amplifier, they have the shape of a negative pulse with a short
rise time ( 20 ns), but a relatively long fall time.
One of these signals will give information about the
amount of energy that was deposited by the incoming gamma quantum, and
the other will be used for determining when the energy was deposited.
20 ns), but a relatively long fall time.
One of these signals will give information about the
amount of energy that was deposited by the incoming gamma quantum, and
the other will be used for determining when the energy was deposited.
The change of the pulse, i.e. the area under the current curve, is
proportional to the deposited energy. Therefore, one of the signals is
processed by a slow linear amplifier (A in Fig 2). This
amplifier gives an output signal of gaussian shape, for which the
amplitude is proportional to the area of the input signal, so that the
energy information that is contained in the input signal is
conserved. There are two other reasons for changing the shape of the
signal. One is improvement of the signal-to-noise ratio, which in
principle means filtering out the the frequencies that are
dominated by noise. By reducing the band width, i.e. removing these
Fourier components from the signal, the shape of the pulse will be
changed. Also, superposition of succeeding signals on the tail of the
first pulse (so-called pile-up) should be avoided, since the pile-up
would distort the energy signal. This can be avoided by reducing the
length of the tail. A linear amplifier consists in principle of a
number of integrating and differentiating steps. Usually, the time
constant of these steps can be varied. Since as much as possible of
the charge of the input signal should be retained, a long integration
time is favorable.
The other output signal from the detector is passed to a quick
amplifier. This device should amplify the signal, optimize the pulse
shape in order to improve the time definition, and reduce the
noise. This is achieved by processing the signal in a number of
filters with a small time constant. The result is a pulse with a very
short rise and fall time. The output signal has a
typical half width of some ten nanoseconds. From the TFA the signal is
passed on to a discriminator.
Figure 3:
``Walk'': Two input signals with the same rise
time pass a given level at different time. The trigger point is
walking and a shift is introduced.
``Jitter'': Overloaded noise also causes a time displacement, but not
as large as the displacement caused by walk.
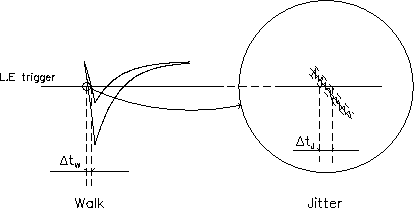 |
The discriminator converts the analogous input signal to a digital
pulse which can then be used for making a digital AND of the two
detector branches. Various types of discriminators exist, and they can
be distinguished by the way the trigger condition is defined. The most
simple form of trigger conditions is the so-called ``leading edge''
(LE) trigger. When the input signal passes a certain level, a digital
pulse is given on the output. The problem with this kind of amplifier
is that signals with the same rise times but different amplitudes will
reach the trigger level at different times, which gives a time
displacement between the two digital pulses that these signals give on
the output. This effect, known as ``walk'' (see
Fig. 3), must be eliminated if the coincidence within
a few nanoseconds between two signals is to be determined. Another
cause for the deterioration of the time characteristics of the signal
is the so-called time jitter which is caused by high
frequency noise on top of the signal. Two identical signals will never
trig at exactly the same time, since the noise causes the trigger
level to be reached at different times. This effect is much smaller than
the former one, since the noise normally has very low amplitude, and
very high frequency as compared to the signal. If a source that emits
two gamma quanta at exactly the same time is used (for example
annihilation radiation from 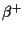 decay) and these two quanta hit
one detector each, measurement of the time between these events will give
information about the size of the time jitter. This can most easily be
done by using one of the signals as a start signal, and the other one
as a stop signals for a time to amplitude converter (TAC, see Krane
ch. 7.7). The output signal from the TAC is proportional to the time
between the start and the stop signal, and can be passed to a MCA. The
half width of the measured curve defines the time resolution of the
system, which also means the times that are shorter than this can not
be distinguished by the system. Another source of time jitter is the
collection of charges in the detector crystal. Depending of where a
quantum has been absorbed in the crystal, the distance that the charge
will have to travel before total collection has been achieved will
vary. This gives a time difference between two simultaneous events.
decay) and these two quanta hit
one detector each, measurement of the time between these events will give
information about the size of the time jitter. This can most easily be
done by using one of the signals as a start signal, and the other one
as a stop signals for a time to amplitude converter (TAC, see Krane
ch. 7.7). The output signal from the TAC is proportional to the time
between the start and the stop signal, and can be passed to a MCA. The
half width of the measured curve defines the time resolution of the
system, which also means the times that are shorter than this can not
be distinguished by the system. Another source of time jitter is the
collection of charges in the detector crystal. Depending of where a
quantum has been absorbed in the crystal, the distance that the charge
will have to travel before total collection has been achieved will
vary. This gives a time difference between two simultaneous events.
A way of avoiding ``walk'' is to have a different trigger level for
signals of different amplitudes. The output signal of the TFA has,
with a good accuracy, a constant rise time and also such a pulse
shape that it takes two signals of different amplitudes the same time
to rise to a given fraction of the maximum amplitude. The CFD uses
this in the following manner (see also Fig. 4):
Figure 4:
The principle of CFD triggering: Signals with the same rise
time can be triggered at the same time if the input signal is divided
into two parts which are treated differently and then added back together.
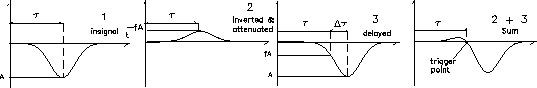 |
The input signal is divided into two parts. One of them is damped to a
fraction 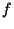 of the total amplitude
of the total amplitude 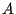 ,
and inverted. The other
signal is delayed a time
,
and inverted. The other
signal is delayed a time 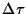 ,
which is the time it takes for
the signal to rise from the amplitude
,
which is the time it takes for
the signal to rise from the amplitude 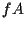 to
to 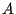 .
This delay can be
adjusted with an external delay cable, so that an optimal trigger
level is created. If these two signals are added, all signals with the
same rise time,
.
This delay can be
adjusted with an external delay cable, so that an optimal trigger
level is created. If these two signals are added, all signals with the
same rise time, 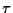 ,
will pass the zero at the same time, and the
time walk of the LE triggering is avoided. However, the time shift
between time signals of different rise times is still present. Since
the difference in rise time usually is small, the shift can be reduced
by making the delay a little bit shorter than
,
will pass the zero at the same time, and the
time walk of the LE triggering is avoided. However, the time shift
between time signals of different rise times is still present. Since
the difference in rise time usually is small, the shift can be reduced
by making the delay a little bit shorter than 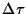 .
Then the
zero cross over will happen before the maximum amplitude is achieved,
which means that the difference in rise time matters less. The width
of the digital pulse from the output of the CFD can be varied. In our
case, it should be around 50 ns. There is also a possibility to set a
lower threshold level. This is done by using the output signal of the
CFD as a trigger pulse on the oscilloscope, and at the same time
looking at energy signal that corresponds to the trigger point. If
pulses are coming from the CFD without any energy signal, the
threshold level must be increased. If the threshold is too high, the
ADCs will be continuously open and the count rate will be so high that
their inputs are blocked. The threshold should be set so that low
energy signals are detected, but high enough to reduce the noise.
.
Then the
zero cross over will happen before the maximum amplitude is achieved,
which means that the difference in rise time matters less. The width
of the digital pulse from the output of the CFD can be varied. In our
case, it should be around 50 ns. There is also a possibility to set a
lower threshold level. This is done by using the output signal of the
CFD as a trigger pulse on the oscilloscope, and at the same time
looking at energy signal that corresponds to the trigger point. If
pulses are coming from the CFD without any energy signal, the
threshold level must be increased. If the threshold is too high, the
ADCs will be continuously open and the count rate will be so high that
their inputs are blocked. The threshold should be set so that low
energy signals are detected, but high enough to reduce the noise.
As is mentioned above, the width of the coincidence window is set by
using the CFD. This width determines within which time interval a pulse
in the other branch of the system much appear for both of the pulses
that are input to the CU to be active at the same time. The life time for a nuclear
level is typically 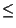 1ns, while the time resolution is around 20
ns. Two gamma quanta that are not separated by a meta stable level can
therefore not be separated in time by the acquisition system. Because
of this, the emission of the two gamma quanta is said to happen
promptly. Ideally, a prompt emission of two gamma quanta should give
two time signals that are sinultaneous, but because of jitter,
this will not happen. This is the reason for the introduction of a
50 ns gate. If this time is reduced, some coincident gamma pairs will
be lost, and if it is too long, the number of random coincidences will
increase. The random coincidences can never be completely avoided,
since two nuclei may decay at the same time. When both of the input
signals to the CU are active, the CU will give a digital pulse, just
like a normal AND gate. However, this can not be used directly
to open the ADCs.
The total signal processing time from when two gamma quanta hits the
detectors until a pulse is available on the output of the CU is some
hundred nanoseconds. The processing of the energy signal, however, is
not finished until after several microseconds. In order to put energy
and gate signals in phase, the gate signal must be delayed, and this
is done in the gate and delay generator (GDG). Also, the pulse length
must be adjusted so that both ADCs are opened when the energy signals
reach their maximum.
1ns, while the time resolution is around 20
ns. Two gamma quanta that are not separated by a meta stable level can
therefore not be separated in time by the acquisition system. Because
of this, the emission of the two gamma quanta is said to happen
promptly. Ideally, a prompt emission of two gamma quanta should give
two time signals that are sinultaneous, but because of jitter,
this will not happen. This is the reason for the introduction of a
50 ns gate. If this time is reduced, some coincident gamma pairs will
be lost, and if it is too long, the number of random coincidences will
increase. The random coincidences can never be completely avoided,
since two nuclei may decay at the same time. When both of the input
signals to the CU are active, the CU will give a digital pulse, just
like a normal AND gate. However, this can not be used directly
to open the ADCs.
The total signal processing time from when two gamma quanta hits the
detectors until a pulse is available on the output of the CU is some
hundred nanoseconds. The processing of the energy signal, however, is
not finished until after several microseconds. In order to put energy
and gate signals in phase, the gate signal must be delayed, and this
is done in the gate and delay generator (GDG). Also, the pulse length
must be adjusted so that both ADCs are opened when the energy signals
reach their maximum.
Figure 5:
Data transfer scheme for the acquisition system
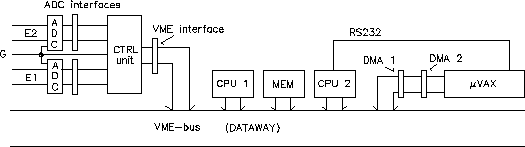 |
When the ADC is opened by the gate pulse, the analogous input
signal is digitized, provided that the acquisition system is ready to
do this. The ADCs can both give 8k, i.e. 8192, output channels. They
are supervised by a control unit via an interface. The control unit is
connected to a VME interface, and is thereby in contact with other
units via a 20 MHz bus (i.e. a fast parallel data cable). When an
event is finished for retrieval from the ADCs, the control unit reads
both energies, and data is transferred via the VME interface by a
processor (CPU 1) to the local memory of the computer
(MEM). Thereafter, the same processor restores the same processor the
interface and the ADCs using the CU and data from a new event can be
collected. In total, the ADCs process the signal during about 20
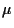 s, while the transferring and restoring takes 40
s, while the transferring and restoring takes 40 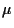 s for the
processor to perform. When the local memory is full, the data is
transferred by a so-called Direct Memory Access unit. It is controlled
by yet another processor (CPU 2). Data can thereafter, independently
of the rest of the system, be transferred to a similar DMA unit which
is placed in the micro Vax which is the host computer for the
acquisition system. The other processor is also in contact with the
host via a serial RS232 cable, over which commands are given to the
acquisition system. In the host, the events are stored both as
integers in a matrix where the row an column indices, respectively,
are the energies and also in one dimensional spectra, which are the
total projections for the two axes of the matrix.
s for the
processor to perform. When the local memory is full, the data is
transferred by a so-called Direct Memory Access unit. It is controlled
by yet another processor (CPU 2). Data can thereafter, independently
of the rest of the system, be transferred to a similar DMA unit which
is placed in the micro Vax which is the host computer for the
acquisition system. The other processor is also in contact with the
host via a serial RS232 cable, over which commands are given to the
acquisition system. In the host, the events are stored both as
integers in a matrix where the row an column indices, respectively,
are the energies and also in one dimensional spectra, which are the
total projections for the two axes of the matrix.
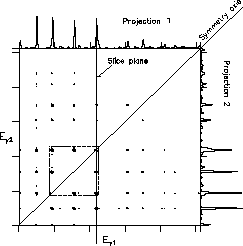
Figure 6:
1/64 of a 4k 4k matrix seen ``from above''. The dashedpart is seen magnified and from the side in Fig. 7.
4k matrix seen ``from above''. The dashedpart is seen magnified and from the side in Fig. 7.
|
|
Figure 7:
Parts of the matrix in Fig. 6 seen magnified
and from above.
|
|
In Fig 6, the total intensity of the matrix
has been projected onto the two axes. The corresponding projections
are used in the lab exercise for finding the energies for all gamma
quanta that are emitted. In the analysis, a slice of the matrix is
taken for each of the peaks in the projection. This slice corresponds
to the slice plane in figure 7. For each
slice, at least one background slice is also set.
The gamma rays that hit the detectors may also Compton scatter out of
the detector. This will result in events where only part of the total
energy has been registered for one or both of the gammas rays.
Parallel to the axes, there is because of this a Compton distribution
for each peak. These ``strings'' of events, which are called Compton
ridges, are clearly visible in
Figure 7. There is also a general background in all
channels, which corresponds to events where both gamma quanta have
scattered. Random coincidences are also part of this background. By
assuming that the background of the peaks in the gate is very similar
to the background next to the peak, the background of the gate peaks
is approximated by the background of corresponding events in the
background gate. By subtracting the background gate from the peak
window, a coincidence spectrum almost without background is
achieved. In the lab exercise, this is done automatically by the
program. Before this, however, the peak and background gates must be
set manually in the matrix.
Some useful information for analyzing coincidence spectra:
- Rotational spectra often contain both M1 transitions and E2
transitions. Two M1 transitions the connect the same states as one E2
transition.
- Mutually exclusive quanta must be placed in separate branches of
the level scheme.
- All transitions in a cascade must ``see'' each other.
- The total sum of intensities of the transitions leading to a
level is the same as the total intensity of the transitions from a level.
- The intensities of the peaks are also dependent on the
efficiency curve.
A report should be written, where all of the above point are discussed.
Torbjörn Bäck
Studies of excited nuclear states by using the 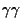 -
coincidence technique
-
coincidence technique
This document was generated using the
LaTeX2HTML translator Version 98.2 beta8 (September 9th, 1998)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 1 gammagamma.tex
The translation was initiated by on 2001-10-12


2001-10-12
![]() and
and ![]() per second and the time gate is
per second and the time gate is ![]() seconds wide, in average
seconds wide, in average
![]() random coincidences are detected each second. By
minimizing the time gate, this number can be kept at an acceptable
level. In some cases a level is metastable, or isomeric, which has
as a consequence that all transitions that are below (or after) this
level will end up outside this time gate if the gate is started by a
transition above this level. In such a case, the levels below and above
the isomeric state can be tied together by increasing the length of
the time gate.
random coincidences are detected each second. By
minimizing the time gate, this number can be kept at an acceptable
level. In some cases a level is metastable, or isomeric, which has
as a consequence that all transitions that are below (or after) this
level will end up outside this time gate if the gate is started by a
transition above this level. In such a case, the levels below and above
the isomeric state can be tied together by increasing the length of
the time gate.


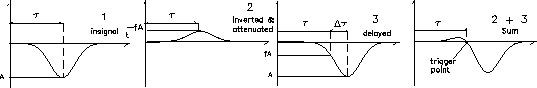
![]() s, while the transferring and restoring takes 40
s, while the transferring and restoring takes 40 ![]() s for the
processor to perform. When the local memory is full, the data is
transferred by a so-called Direct Memory Access unit. It is controlled
by yet another processor (CPU 2). Data can thereafter, independently
of the rest of the system, be transferred to a similar DMA unit which
is placed in the micro Vax which is the host computer for the
acquisition system. The other processor is also in contact with the
host via a serial RS232 cable, over which commands are given to the
acquisition system. In the host, the events are stored both as
integers in a matrix where the row an column indices, respectively,
are the energies and also in one dimensional spectra, which are the
total projections for the two axes of the matrix.
s for the
processor to perform. When the local memory is full, the data is
transferred by a so-called Direct Memory Access unit. It is controlled
by yet another processor (CPU 2). Data can thereafter, independently
of the rest of the system, be transferred to a similar DMA unit which
is placed in the micro Vax which is the host computer for the
acquisition system. The other processor is also in contact with the
host via a serial RS232 cable, over which commands are given to the
acquisition system. In the host, the events are stored both as
integers in a matrix where the row an column indices, respectively,
are the energies and also in one dimensional spectra, which are the
total projections for the two axes of the matrix.