The Mössbauer Effect in 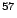 Fe
Fe
Laboratory Exercise in Nuclear Physics
Autumn 2005
Before starting the lab exercise you should read chapter 10.9 in
K.S. Krane Introductory Nuclear Physics.
To get a high quality printed version of this lab instruction
you can use the postscript
version.
When an excited nucleus decays by emitting a gamma ray, this gamma ray
might be absorbed by another nucleus, but only if there in that
nucleus exists a transition with exactly the correct energy. This
resonant absorption can usually not take place if the nuclei are of
the same kind, since the nuclei will recoil. The recoil will cause the
energy of an emitted gamma ray to be slightly lower than the energy of
the corresponding transition, and if a gamma ray is to be absorbed,
its energy has to be slightly higher than the transition energy. This
shift in energy is several orders of magnitude larger than the
intrinsic width of the resonance, and therefore the resonant
absorption of a emitted gamma ray usually is not possible, even if the
absorbing and emitting nuclei are of the same kind. The shift caused
by the recoil of nuclei is also known from atomic physics, but there
the shift is much smaller since the transition energies and therefore
the recoil energies are much lower than in the case of nuclear
physics.
In 1958, Rudolph Mössbauer discovered that some of the nuclei in the
crystal that he studied could emit and absorb a light quantum without
absorption or emission of a phonon. This means that the crystal will
be in the same internal state before and after the event. The recoil
is taken up by the crystal as a whole, and not by the individual
atom, which makes the recoil energy, and thereby the shift in energy
for the gamma ray, immeasurably small. Therefore, a photon emitted in
such a way can be absorbed by an identical nucleus, provided that also
this nucleus is bound in a crystal.
The probability for this absorption without recoil
increases with decreasing temperature, and
usually only a small fraction of the gamma rays are absorbed and
emitted recoilless at room temperature. However, in the case of
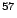 Fe in steel, which will be studied in this lab exercise, as much
as 14% of the absorbed gamma photons are absorbed recoil free at room
temperature.
Fe in steel, which will be studied in this lab exercise, as much
as 14% of the absorbed gamma photons are absorbed recoil free at room
temperature.
Assume that a nucleus absorbs a gamma quantum. The conservation of
energy and momentum gives:
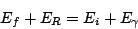 |
(1) |
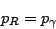 |
(2) |
If these two equations are combined, the result is:
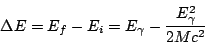 |
(3) |
This means that the energy has been shifted an amount 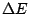 towards higher energies. However, because of the natural line width,
gamma ray absorption may occur for energies that differ slightly from
this value. Every excited state has a life time,
towards higher energies. However, because of the natural line width,
gamma ray absorption may occur for energies that differ slightly from
this value. Every excited state has a life time, 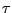 , and therefore
a natural line width
, and therefore
a natural line width
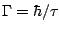 . For low-lying states,
this width is between
. For low-lying states,
this width is between 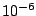 and
and 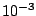 eV.
eV.
In addition to the natural line width, there is also the Doppler
broadening. The Doppler width is caused by the thermal motion of the
absorbing and emitting nuclei, and can be expressed as:
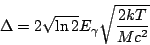 |
(4) |
The Doppler width is usually a couple of orders of magnitude larger
than the natural line width. The two widths combine to give a total
line width 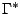 , where
, where
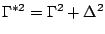 . The
gamma ray absorption cross section is then:
. The
gamma ray absorption cross section is then:
![\begin{displaymath}
\sigma(E_\gamma) = \sigma_0 \frac{(\Gamma^*/2)^2}{[E_\gamma-(\Delta
E+E_R)]^2+(\Gamma^*/2)^2}
\end{displaymath}](img14.png) |
(5) |
where 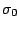 is the absorption cross section for gamma rays of
energy
is the absorption cross section for gamma rays of
energy 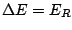 .
.
In a simplified picture, the atoms
in the crystal can be assumed to move with velocities that are
Maxwell distributed:
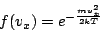 |
(6) |
This movement results in a Doppler shift in any emitted gamma ray:
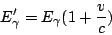 |
(7) |
which gives an energy distribution that is given by:
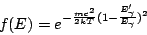 |
(8) |
For the absorption, the distribution is centered around
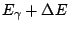 , and for the emission around
, and for the emission around
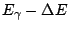 . The area of the overlapping part of the peaks
(see figure 1)
can be changed by changing the temperature of the source
and/or the absorber.
. The area of the overlapping part of the peaks
(see figure 1)
can be changed by changing the temperature of the source
and/or the absorber.
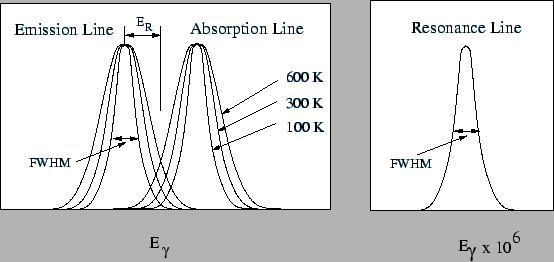
Figure 1:
The left picture shows how the width of the emission and
absorption lines will change with increasing temperature. E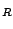 represents the recoil energy. A resonance line,
which is not Doppler broadened, would only be a straight line in this plot.
If the energy scale is a million times enlarged, a resonance line
will look as in the right plot.
represents the recoil energy. A resonance line,
which is not Doppler broadened, would only be a straight line in this plot.
If the energy scale is a million times enlarged, a resonance line
will look as in the right plot.
 |
When Rudolf Mössbauer studied the resonant absorption of  Ir,
he found something interesting. He looked at the absorption as a function
of temperature. When decreasing the temperature of the source and
absorber he expected to see a decreased absorbtion (at lower temperature
the Doppler broadened peaks of figure 1 overlap less).
But to his surprise he found an increase of the absorption.
He could explain the new effect when he realized that part of the
nuclei can emit or receive a gamma photon without recoil.
Ir,
he found something interesting. He looked at the absorption as a function
of temperature. When decreasing the temperature of the source and
absorber he expected to see a decreased absorbtion (at lower temperature
the Doppler broadened peaks of figure 1 overlap less).
But to his surprise he found an increase of the absorption.
He could explain the new effect when he realized that part of the
nuclei can emit or receive a gamma photon without recoil.
From the above we see that the Mössbauer effect has
two characteristic features:
- The absorption is recoil free.
- The emission and absorption lines have no Doppler broadening.
In order to simplify the calculations that will be done during the lab
exercise, a short description of the nuclear moments and their
interaction with the electro-magnetic field is included.
Both the magnetic vector potential and the electric potential are
given by integrals over current and charge distributions:
By Taylor expanding the denominator, a so-called multiple expansion
of the potential is obtained.
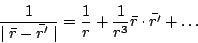 |
(11) |
This can be used in combination with Gauss theorem in the quantum
mechanical case to show that:
where
The dominating term in the expansion of the vector potential will be
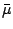 . If the wave function is an eigenstate of
. If the wave function is an eigenstate of 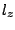 , only
this term will survive the integration. Furthermore, we know that it's
eigenvalue is
, only
this term will survive the integration. Furthermore, we know that it's
eigenvalue is 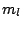 . Therefore:
. Therefore:
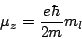 |
(16) |
For 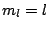 we define:
we define:
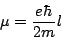 |
(17) |
where 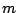 is the nuclear mass. The nuclear magneton is defined as:
is the nuclear mass. The nuclear magneton is defined as:
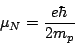 |
(18) |
where 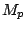 is the mass of a proton. In a similar was as for the spin
of the electron, a g-factor is introduced so that:
is the mass of a proton. In a similar was as for the spin
of the electron, a g-factor is introduced so that:
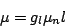 |
(19) |
For the total angular momentum of the nucleus, I, the expression is
analogically:
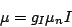 |
(20) |
The energy for a magnetic dipole in a magnetic field is given by:
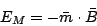 |
(21) |
This gives in our case:
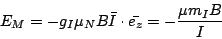 |
(22) |
For the electrical potential, the first term gives the contribution
from the total charge. The second term is zero, since the integrand is
an odd function. The third term gives the quadrupole moment of the
nucleus (see Krane). The electrical quadrupole moment gives a
splitting of the energy levels if the nucleus is placed in an
electrical field gradient. This gradient may for example stem from the
atoms in the lattice, and is then dependent on the symmetry of the
lattice. If the charge distribution is in an external potential,
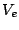 , the electrostatic energy is given by:
, the electrostatic energy is given by:
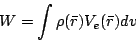 |
(23) |
If the external potential is expanded in a Taylor series, the result
is:
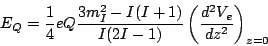 |
(24) |
Figure 2:
The equipment used to study the Mössbauer effect.
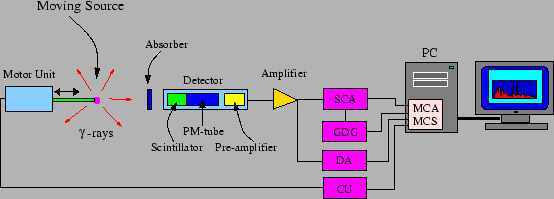 |
The experimental equipment includes a source and an absorber. The
absorber is placed in between the detector and the source. The speed
of the source is varied in a well-controlled manner, so that the
energy of the emitted gamma ray also changes, because of the Doppler
effect. The variation will be over a narrow interval, which is some
ten natural line widths. When a resonance occurs in the absorber, the
number of detected gamma rays will decrease. By gating on this energy,
the SCA gives a digital pulse every time a light quantum with the
correct energy hits the detector. Therefore it is enough to count how the
number of pulses per unit of time decreases at the resonance. In a MCS
spectrum, this can be seen as a decrease in intensity in the channel
that corresponds to this time. Since the time dependence of the velocity
is known, the velocity that corresponds to this channel is also known,
and therefore the Doppler shift of the corresponding radiation can be
calculated. For this to work in practice, the velocities must have the
same duration. Otherwise, one would get a varying intensity. Another
way of saying this is:
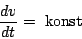
Therefore, the position of the source must be a quadratic function of
the time. In this lab exercise, the velocity has a triangular shape
as a function of time, which means that the source will have the same
velocity twice during one period of motion. Therefore, the spectrum will
be doubled.
The single channel analyzer determines whether the height of its input
signal is between two limits. If the signal is lower than the lower
limit or higher than the upper limit, no output signal is
given. Otherwise, a digital pulse is given as output. The interval
inside which the signal is accepted is called the gate of the
analyzer. The levels are adjusted using the potentiometers called LLD
(Lower Level Dicsriminator) and ULD (Upper Level Discriminator),
respectively. The SCA can also be set to another mode, in which the
size of the gate is set to a fixed value. The entire gate can then
be moved. In either case, the output signal isn't activated until the
input signal has passed the lower trigger level the second
time. This means that the output signal will be delayed with respect
to the input signal.
This unit is triggered by an incoming pulse, and creates a gate pulse
with variable length as output. This can be used to create a digital
pulse of variable length as output. As the name of the device
suggests, it can also be used to delay the pulse.
The output signal can be used in other units, which demand digital
input signals with a certain pulse length as input. In this
lab exercise, the signal will be used to create a coincidence, i.e. make
a multi channel analyzer (see below) only accept energy pulses that
fall within an interval which is determined by a single channel analyzer.
To create a delayed pulse, cables of a well-defined length are often
used. They can also be integrated in certain amplifiers, which in that
case will provide amplification as well as the possibility to choose
between some different delay times.
The amplifier is designed to increase the amplitude of the input
signal, without losing the information contained in the signal. The
amplifier that will be used in the lab exercise has two outputs, one in
the front and one at the back of the box. This makes it possible to
divide the signal in two branches, which can be treated differently.
In this lab exercise, we use a MCA card
which is mounted inside a PC. On the back of this device, there are two
inputs that are of interest. The energy signal should be connected to
the input marked ADC. If a digital pulse is connected to the GATE
input, only those energy signals that are coincident with the GATE
signal will be registered by the MCA. The Maestro software
will be used as an interface for the acquisition system.
A unit that only counts the number of pulses on the input is called a
scaler. Usually, the amplitude of the input signal must be
within a certain interval to be registered. A multi channel scaler can
be regarded as a multi channel analyzer, in which every channel is an
independent counter. If every channel is active during a given
interval of time, after which the closest higher channel is activated
instead, it is possible to display the number of input pulses as a
function of the time. To use the MCS on the PC, a special program is
used. The input signal to the MCS-function in connected to the
TTL-input.
The DAC ouput on the PC is connected to a driving unit, so that the
computer can control the movement of the source. In this case, the
CU will send a triangular signal to the engine. From the engine, a
signal is fed back into the driving unit. This signal is the
difference between the signal emitted by the computer and the true
movements of the source. By checking this signal on an oscilloscope, it
is possible to deduce whether the source is moving the way it should.
Figure 3:
The figure shows the level scheme for  Fe.
Fe.
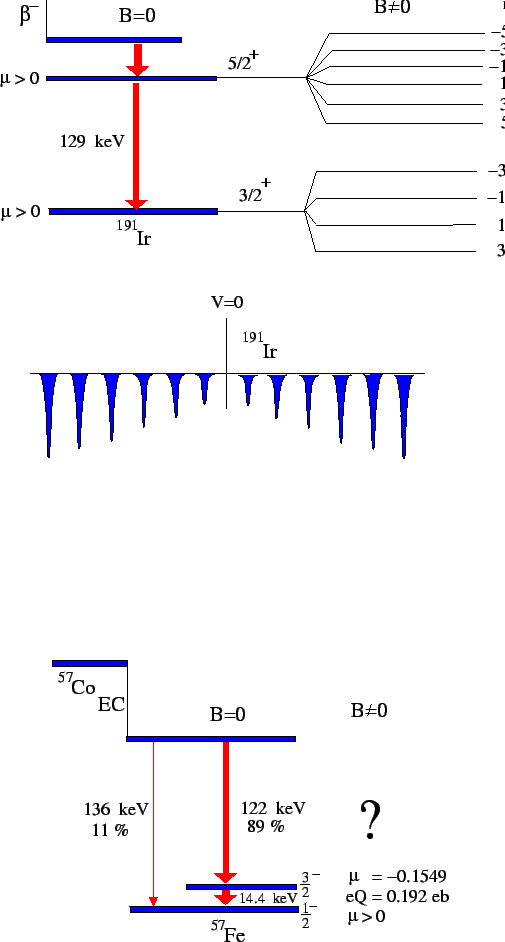 |
The task of this lab exercise is to measure the self-absorption of
the 14.4 keV line in 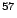 Fe. As can be seen in figure 3,
this transition is from a
Fe. As can be seen in figure 3,
this transition is from a 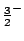 state that is populated
after electron capture (EC) in
state that is populated
after electron capture (EC) in 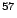 Co. The final state of the
transition is the ground state, which has the spin and parity
Co. The final state of the
transition is the ground state, which has the spin and parity
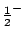 .
Resonance
Firstly, set the gate on the single-channel analyzer. The MCA program
in the PC can be used for doing this. When the gate is set, connect
the signal from the SCA to the PC, and start the multi scaler
program. The measurements will be done with three different absorbers:
.
Resonance
Firstly, set the gate on the single-channel analyzer. The MCA program
in the PC can be used for doing this. When the gate is set, connect
the signal from the SCA to the PC, and start the multi scaler
program. The measurements will be done with three different absorbers:
- Stainless steel
- Natural iron
- FeSO
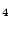
These three samples contain 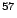 Fe in different environments. The
first one, stainless steel, does not give any splitting of the energy
levels. The natural iron is ferro magnetic, and the magnetic field
inside a domain is very strong. The magnetic moment of the nucleus
will give a splitting of the energy levels in this field. The spin and
parity of the initial and final states are known, but not the
magnitude of
Fe in different environments. The
first one, stainless steel, does not give any splitting of the energy
levels. The natural iron is ferro magnetic, and the magnetic field
inside a domain is very strong. The magnetic moment of the nucleus
will give a splitting of the energy levels in this field. The spin and
parity of the initial and final states are known, but not the
magnitude of 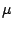 in the ground state, which gives two possibilities
when it comes to identifying the transitions.
in the ground state, which gives two possibilities
when it comes to identifying the transitions.
In the last specimen, FeSO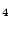 , the nucleus sits in an environment with a
electric field gradient. The electrical quadrupole moment will because
of this split the energy levels in a different way than for the
magnetic dipole moment. This is known:
, the nucleus sits in an environment with a
electric field gradient. The electrical quadrupole moment will because
of this split the energy levels in a different way than for the
magnetic dipole moment. This is known:
-
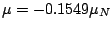 in the 14.4 keV excited state.
in the 14.4 keV excited state.
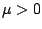 in the ground state
in the ground state
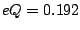 eb for the excited state.
eb for the excited state.
Solve the following problems:
- Calculate the life time for the 14 keV state by measuring with
the first absorber.
- Change to the second absorber. Which transitions are now
possible and why?
- Calculate the magnetic field and
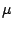 for the ground state.
for the ground state.
- Finally, how are the levels split in the case of the last absorber?
- Calculate the electric field gradient.
The Mössbauer Effect in 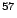 Fe
Fe
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 mossbauer.tex
The translation was initiated by on 2005-09-19
2005-09-19
![]() Fe in steel, which will be studied in this lab exercise, as much
as 14% of the absorbed gamma photons are absorbed recoil free at room
temperature.
Fe in steel, which will be studied in this lab exercise, as much
as 14% of the absorbed gamma photons are absorbed recoil free at room
temperature.

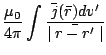
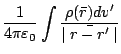
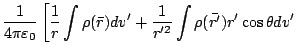
![$\displaystyle \left.+\frac{1}{2r^3}\int\rho(\bar{r'})r'^2(3\cos^2\theta-1)dv'+\ldots\right]$](img32.png)
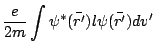
![]() . If the wave function is an eigenstate of
. If the wave function is an eigenstate of ![]() , only
this term will survive the integration. Furthermore, we know that it's
eigenvalue is
, only
this term will survive the integration. Furthermore, we know that it's
eigenvalue is ![]() . Therefore:
. Therefore:
![]() , the electrostatic energy is given by:
, the electrostatic energy is given by:
![]() Fe. As can be seen in figure 3,
this transition is from a
Fe. As can be seen in figure 3,
this transition is from a ![]() state that is populated
after electron capture (EC) in
state that is populated
after electron capture (EC) in ![]() Co. The final state of the
transition is the ground state, which has the spin and parity
Co. The final state of the
transition is the ground state, which has the spin and parity
![]() .
Resonance
Firstly, set the gate on the single-channel analyzer. The MCA program
in the PC can be used for doing this. When the gate is set, connect
the signal from the SCA to the PC, and start the multi scaler
program. The measurements will be done with three different absorbers:
.
Resonance
Firstly, set the gate on the single-channel analyzer. The MCA program
in the PC can be used for doing this. When the gate is set, connect
the signal from the SCA to the PC, and start the multi scaler
program. The measurements will be done with three different absorbers:
![]() Fe in different environments. The
first one, stainless steel, does not give any splitting of the energy
levels. The natural iron is ferro magnetic, and the magnetic field
inside a domain is very strong. The magnetic moment of the nucleus
will give a splitting of the energy levels in this field. The spin and
parity of the initial and final states are known, but not the
magnitude of
Fe in different environments. The
first one, stainless steel, does not give any splitting of the energy
levels. The natural iron is ferro magnetic, and the magnetic field
inside a domain is very strong. The magnetic moment of the nucleus
will give a splitting of the energy levels in this field. The spin and
parity of the initial and final states are known, but not the
magnitude of ![]() in the ground state, which gives two possibilities
when it comes to identifying the transitions.
in the ground state, which gives two possibilities
when it comes to identifying the transitions.
![]() , the nucleus sits in an environment with a
electric field gradient. The electrical quadrupole moment will because
of this split the energy levels in a different way than for the
magnetic dipole moment. This is known:
, the nucleus sits in an environment with a
electric field gradient. The electrical quadrupole moment will because
of this split the energy levels in a different way than for the
magnetic dipole moment. This is known: