Internal Conversion
Laboratory Exercise in Nuclear Physics
Autumn 2005
This laboratory exercise deals with a method of measuring the multi-polarity of
a 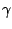 transition in an atomic nucleus. By measuring (indirectly)
the relative intensity of conversion electrons to
transition in an atomic nucleus. By measuring (indirectly)
the relative intensity of conversion electrons to 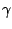 radiation,
the multi-polarity will be deduced.
radiation,
the multi-polarity will be deduced.
Before the lab. exercise you should read
the following parts in the Krane
textbook (K.S. Krane, Introductory Nuclear Physics).
- Angular Momentum and Parity Selection Rules for
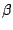 Decay (Krane, chapter 9.4)
Decay (Krane, chapter 9.4)
- Angular Momentum and Parity Selection Rules for
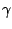 Decay (Krane, chapter 10.4)
Decay (Krane, chapter 10.4)
- Internal Conversion (Krane, chapter 10.6)
- Auger Effect (Any textbook in Atomic Physics, for example: Ch. 18.7 in Haken & Wolf, The Physics of Atoms and Quanta.)
- Semiconductor Detectors (Krane, chapter 7.4)
To get a high quality printed version of this lab instruction
you can use the pdf
version.
This section will explain some basics about the interaction
between particles and materials. To understand the
techniques used to detect the particles emitted from a nucleus
or an atom it is neccessary to understand these processes.
When a charged particle enters a material it will slow down
and also change direction. The electric field of the particle
will excite electrons to higher states or will free bound electrons
from the atoms in the material . If an electron gets
enough energy to travel
through the material it can excite other electrons, so-called
secondary electrons. The possible ways of excitation depend
on the material. In a gas-detector the main idea is to
generate electron-ion pairs. These free charges can then be
collected by applying an external voltage. In a semiconductor
the idea is to excite electrons from the valence band into the
conduction band creating electron-hole pairs. An applied voltage
can also in this case extract the created charge. In scintillating
materials the excited electrons will de-excite, sending out
photons. The light can be collected and amplified with a
photomultiplier, creating an electronic pulse.
The general expression for the change in energy per distance,
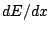 , for a charged particle slowing down in a material
is called Bethe-Blochs formula and is given by:
, for a charged particle slowing down in a material
is called Bethe-Blochs formula and is given by:
![\begin{displaymath}
-\frac{dE}{dx}=\left(\frac{e^2}{4\pi\epsilon_0}\right)^2
\fr...
...2}{I}\right)-
ln(1-\beta^2)-\beta^2-\delta-\frac{C}{Z}\right],
\end{displaymath}](img7.png) |
(1) |
where:
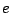 is the electron charge
is the electron charge
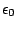 is the permeability in vacuum
is the permeability in vacuum
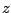 is the incoming particle's charge in
is the incoming particle's charge in 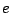
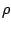 is the density of the material
is the density of the material
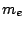 is the electron mass
is the electron mass
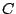 is the shell correction parameter
is the shell correction parameter
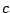 is the speed of light
is the speed of light
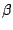 is
is 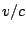 for the incoming particle
for the incoming particle
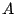 is the molar mass of the material
is the molar mass of the material
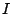 is the mean excitation potential
is the mean excitation potential
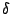 is a density correction term
is a density correction term
Note that 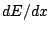 is proportionated to
is proportionated to 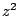 . This means for
example that an alpha particle will stop much faster
compared to a proton in a given material.
. This means for
example that an alpha particle will stop much faster
compared to a proton in a given material.
There are resons why the electron (and the positron) must be treated
differently from the other charged particles. One reason is the small
mass. One of the assumptions of the Bethe-Blochs formula is that the
mass of the incoming particle is much larger
than the mass of the electrons in the material.
We therefore assume the particle to move in the same direction
after interacting with an electron. This can be a good
approximation for incoming protons or 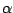 particles, but not
for electrons. Another difference is that two colliding electrons
are not separable. A quantum mechanical treatment of the problem
therefore introduces new terms for the electrons.
particles, but not
for electrons. Another difference is that two colliding electrons
are not separable. A quantum mechanical treatment of the problem
therefore introduces new terms for the electrons.
Apart from the inelastic scattering against other electrons, another
mechanism will also be important, namely emission of Bremsstrahlung.
This emission of electromagnetic radiation is due to the deceleration
of the electrons when they enter the material. The cross section
for Bremsstrahlung is dependent on the mass as:
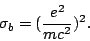 |
(2) |
We se that Bremsstrahlung is more important for high energies, and that
it must be much more important for electrons than for heavier particles
like protons or 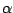 -particles. For electrons at an energy of
about 10 MeV, the Bremsstrahlung effect is about as large as the effect
from inelastic scattering.
-particles. For electrons at an energy of
about 10 MeV, the Bremsstrahlung effect is about as large as the effect
from inelastic scattering.
A 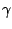 -photon can interact with a material in three ways:
-photon can interact with a material in three ways:
- Photo absorption
- Compton scattering
- Pair production
The 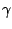 -photon can be absorbed completely by giving
all its energy to an electron in the material.
This electron will have the same energy as the photon
(except for the small binding energy). The electron
will then excite many other so-called secondary electrons.
The total energy of these electrons corresponds
to the photon energy, so if we can measure this total
energy we get the photon energy.
If the photon only gives part of its energy to
an electron in the material, the photon will continue
to travel through the material, but in a new direction
and with a lower energy. It can then be photo-absorbed,
it can Compton scatter again, or it can escape from the material
(for example from a detector). The electron that were hit will
excite other electrons in the material. If the scattered photon
ecapes from the detector, the total electron energy will be
lower than the energy of the incoming photon. In this case,
the measured energy does not correspond to the
-photon can be absorbed completely by giving
all its energy to an electron in the material.
This electron will have the same energy as the photon
(except for the small binding energy). The electron
will then excite many other so-called secondary electrons.
The total energy of these electrons corresponds
to the photon energy, so if we can measure this total
energy we get the photon energy.
If the photon only gives part of its energy to
an electron in the material, the photon will continue
to travel through the material, but in a new direction
and with a lower energy. It can then be photo-absorbed,
it can Compton scatter again, or it can escape from the material
(for example from a detector). The electron that were hit will
excite other electrons in the material. If the scattered photon
ecapes from the detector, the total electron energy will be
lower than the energy of the incoming photon. In this case,
the measured energy does not correspond to the 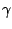 -ray energy.
If the
-ray energy.
If the 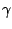 -photon has enough energy, it can
interact with the electromagnetic field of a nucleus and
create a electron-positron pair. The positron will soon find
an electron in the material and this electron
will annihilate with the positron after a short time, creating two
511 keV
-photon has enough energy, it can
interact with the electromagnetic field of a nucleus and
create a electron-positron pair. The positron will soon find
an electron in the material and this electron
will annihilate with the positron after a short time, creating two
511 keV 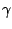 -photons.
A discrete state in an atomic nucleus is characterised
by (among other things) its parity, and its spin.
If we can determine the spin and
parity experimentally, we can learn something about the inner
structure of the nucleus (using a given model).
It is therefore important to find ways of deducing the spin
and parity for the different states of the nucleus.
-photons.
A discrete state in an atomic nucleus is characterised
by (among other things) its parity, and its spin.
If we can determine the spin and
parity experimentally, we can learn something about the inner
structure of the nucleus (using a given model).
It is therefore important to find ways of deducing the spin
and parity for the different states of the nucleus.
To find information about the different states of
a nucleus we study the transitions between the states.
A transition from one state to a energetically lower state
will result in the emission of energy from the nucleus.
This energy is usually emitted in the form of a 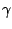 photon,
but the nucleus can also interact with the electrons of its atom
to release the excess energy.
photon,
but the nucleus can also interact with the electrons of its atom
to release the excess energy.
A 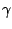 photon emitted from a nucleus will have an energy corresponding
to the difference in energy between the initial and final state of the nucleus.
The multipolarity of the photon corresponds to the angular momentum
that the photon carries away from the nucleus. If we know the
spin and parity of one of the states, we can learn something
about the spin and parity of the other state by measuring
the multipolarity of the emitted photon.
photon emitted from a nucleus will have an energy corresponding
to the difference in energy between the initial and final state of the nucleus.
The multipolarity of the photon corresponds to the angular momentum
that the photon carries away from the nucleus. If we know the
spin and parity of one of the states, we can learn something
about the spin and parity of the other state by measuring
the multipolarity of the emitted photon.
The multipolarity of a nuclear transition can be measured in various ways.
One striking difference between different multipolarities is the
angular intensity distribution of the radiation. The distribution
is given by the Legendre polynomials of the corresponding order. The distribution
of the radiation for one transition will only give us information
about the order of the transition, it is not possible to
see if the transition is magnetic or electric. To do this we
also need to measure the polarisation of the radiation.
Figure 1:
The degenerated energy levels can be separated by a magnetic field.
Each component in the decay will then have a specific angular distribution.
But if the sub-levels are evenly populated the sum distribution will
be isotropic.
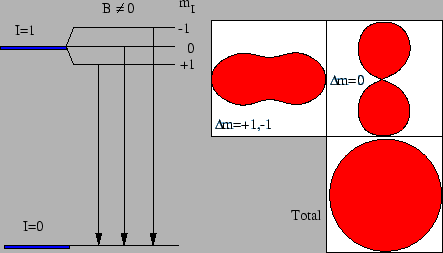 |
To get an non-isotropic intensity distribution, the magnetic sub-levels
must be unevenly populated. Assuming, see figure 1 that
an I=1 state is de-excited into an I=0 state, we have three possible
transitions corresponding to the three magnetic sublevels for I=1.
Each transition have a different 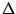 m, and therefore a different
angular intensity distribution. The problem is that is is not trivial
to separate the three transitions. We can split up the levels by
applying an external magnetic field, but even a very large field
will not make it possible to separate the transitions with a
normal
m, and therefore a different
angular intensity distribution. The problem is that is is not trivial
to separate the three transitions. We can split up the levels by
applying an external magnetic field, but even a very large field
will not make it possible to separate the transitions with a
normal 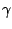 -ray detector. We will therefore see a sum of the
three angular distributions, and if the sub-levels are evenly
populated the sum will be isotropic. One way to solve the
problem is to lower the temperature
of the source so that the Boltzmann distribution will give an
uneven distribution of the population of the sub-levels. To
do this, the temperature must be as low as about 0.01 K.
-ray detector. We will therefore see a sum of the
three angular distributions, and if the sub-levels are evenly
populated the sum will be isotropic. One way to solve the
problem is to lower the temperature
of the source so that the Boltzmann distribution will give an
uneven distribution of the population of the sub-levels. To
do this, the temperature must be as low as about 0.01 K.
We see that there are several difficulties in using the intensity
distribution for measuring the multipolarity of a nuclear transition.
There are however other ways of solving these difficulties, like
using so-called angular correlation measurements (Krane, ch. 10.4).
In this laboration we will use another technique to measure the
multipolarity of a transition. This method does not depend on
the angular intensity distribution of the 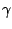 radiation.
Instead, we use the fact that
the the relative intensity of internal conversion
depend on the multipolarity of the transition (the intensity
does also depend on other factors, see Krane, page 346).
By measuring the internal
conversion intensity, we can therefore deduce the multipolarity of the
transition.
radiation.
Instead, we use the fact that
the the relative intensity of internal conversion
depend on the multipolarity of the transition (the intensity
does also depend on other factors, see Krane, page 346).
By measuring the internal
conversion intensity, we can therefore deduce the multipolarity of the
transition.
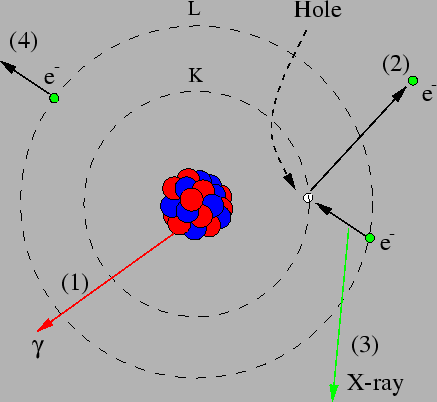
Figure 2:
A schematic picture of different ways to de-excite an atomic nucleus. The nucleus can be de-excited by 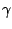 -ray emission (1), but also
by emitting a closely bound electron from the atom (2). Usually a K-electron
is emitted, but an electron in the L-shell (or a higher
shell) can also be emitted. The electron hole
that appears will soon be filled by another electron. This can
result in the emission of an X-ray photon (3), or the emission
of an Auger electron (4).
-ray emission (1), but also
by emitting a closely bound electron from the atom (2). Usually a K-electron
is emitted, but an electron in the L-shell (or a higher
shell) can also be emitted. The electron hole
that appears will soon be filled by another electron. This can
result in the emission of an X-ray photon (3), or the emission
of an Auger electron (4).
 |
The internal conversion coefficient is defined as:
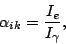 |
(3) |
where 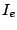 is the intensity of the conversion electrons and
is the intensity of the conversion electrons and 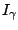 is the intensity of the gamma radiation.
is the intensity of the gamma radiation. 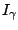 can easily be
determined by calculating the area of the corresponding peak in the
energy spectrum. To determine the intensity of the conversion electrons
we will not measure the electrons directly in this case (for doing
this we would need an electron detector). Instead, we will measure
the intensity of the X-ray radiation that is sent out when the electron
holes (created by sending out the conversion electrons)
are filled by electrons from higher lying shells. This intensity
must however be corrected to account for the Auger effect, since
this process competes with X-ray emission. The ratio between the
X-ray intensity
can easily be
determined by calculating the area of the corresponding peak in the
energy spectrum. To determine the intensity of the conversion electrons
we will not measure the electrons directly in this case (for doing
this we would need an electron detector). Instead, we will measure
the intensity of the X-ray radiation that is sent out when the electron
holes (created by sending out the conversion electrons)
are filled by electrons from higher lying shells. This intensity
must however be corrected to account for the Auger effect, since
this process competes with X-ray emission. The ratio between the
X-ray intensity 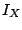 and the intensity of internal conversion
and the intensity of internal conversion 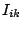 is given as:
is given as:
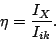 |
(4) |
Diagrams for 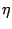 can be found in appendix A.
can be found in appendix A.
Another problem is that we must compensate for the efficiency
of the detector. This efficiency is energy dependent, so an
efficiency curve can be plotted by measuring the intensities
of some 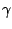 -ray peaks for a number of calibration sources. Using
the efficiency curve, the ratio between the detector efficiencies
for the X-rays and
-ray peaks for a number of calibration sources. Using
the efficiency curve, the ratio between the detector efficiencies
for the X-rays and 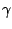 -rays of interest can be measured as:
-rays of interest can be measured as:
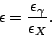 |
(5) |
By combining the relations above we can now calculate 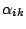 .
Diagrams that relate
.
Diagrams that relate 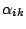 to energy and multi-polarity can be
found in the laboratory.
From this multi-polarity we can conclude the spin and parity
for the 662 keV state of
to energy and multi-polarity can be
found in the laboratory.
From this multi-polarity we can conclude the spin and parity
for the 662 keV state of 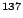 Ba by using the selection rules.
Ba by using the selection rules.
A schematic picture of the detector set-up of the present lab exercise
is seen in figure 3. A radioactive source is put in front
of a germanium detector. The source will emit 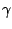 -rays from nuclear
de-excitation, and also X-rays that originate from internal conversion.
The germanium detector must be cooled to low temperature by liquid nitrogen.
The electronic signal from the detector is fed into an amplifier and then
to a multi-channel analyser (MCA) that can sort the signal into a large
number of energy channels. The Maestro PC software is then used
to display and analyse the energy spectrum.
-rays from nuclear
de-excitation, and also X-rays that originate from internal conversion.
The germanium detector must be cooled to low temperature by liquid nitrogen.
The electronic signal from the detector is fed into an amplifier and then
to a multi-channel analyser (MCA) that can sort the signal into a large
number of energy channels. The Maestro PC software is then used
to display and analyse the energy spectrum.
Figure 3:
The detector set-up of the present laboration.
|
|
In the present laboration we use a source of 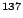 Cs to
study internal conversion. The
Cs to
study internal conversion. The 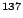 Cs nucleus decays
by
Cs nucleus decays
by 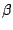 -decay into two different states in
-decay into two different states in
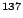 Ba (figure 4).
Ba (figure 4).
Figure 4:
The decay of 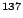 Cs into two states of
Cs into two states of  Ba. The
purpose of the lab. exercise is to determine the spin and
parity of the excited 662 keV state of
Ba. The
purpose of the lab. exercise is to determine the spin and
parity of the excited 662 keV state of  Ba.
Ba.
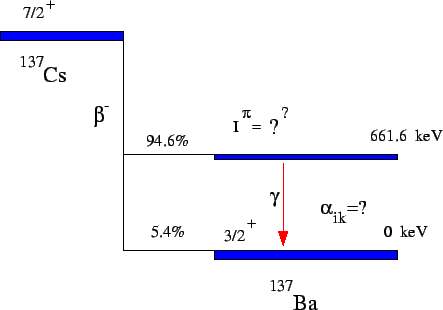 |
One of these states is the ground state, the other is an
excited state, 662 keV above the ground state.
The MCA PC card is controlled by the Maestro software on the PC.
Put a source (for example  Co) in front of the
NaI detector
and start the acquisition system from within Maestro.
Try to explain what you see in the different parts of the spectrum.
Then, do the same thing with the germanium detector.
What is the most striking difference between the two detector types?
Co) in front of the
NaI detector
and start the acquisition system from within Maestro.
Try to explain what you see in the different parts of the spectrum.
Then, do the same thing with the germanium detector.
What is the most striking difference between the two detector types?
The multichannel analyser (MCA) is not energy calibrated before
the lab. exercise. We must therefore use a few of the known energies
of the calibration sources to calibrate the MCA.
To determine the conversion coefficient 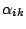 we must first
measure the efficiency of the detector as a function of energy.
This is done by using the known intensity for a number
of
we must first
measure the efficiency of the detector as a function of energy.
This is done by using the known intensity for a number
of 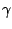 -transitions in a few calibration sources. The
half-lifes and reltive gamma intensities are found in table 1.
-transitions in a few calibration sources. The
half-lifes and reltive gamma intensities are found in table 1.
Table 1:
Half-lifes, energies, and intensities for a few calibration sources.
| Source |
Half-life |
E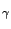 (keV) (keV) |
I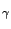 (%) (%) |
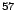 Co Co |
271.7 d |
14.4 |
9.2 |
| |
|
122.1 |
85.6 |
| |
|
136.5 |
10.7 |
 Am Am |
432 y |
26.3 |
2.4 |
| |
|
59.5 |
36.0 |
 Ba Ba |
10.52 y |
81.0 |
34.1 |
| |
|
276.4 |
7.1 |
| |
|
302.9 |
18.3 |
| |
|
356.0 |
61.9 |
| |
|
383.8 |
8.9 |
 Na Na |
2.6019 y |
1274.5 |
99.9 |
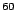 Co Co |
5.2714 y |
1173.2 |
99.9 |
| |
|
1332.5 |
100.0 |
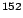 Eu Eu |
13.542 y |
121.8 |
28.4 |
| |
|
244.7 |
7.5 |
| |
|
344.3 |
26.6 |
| |
|
411.1 |
2.2 |
| |
|
444.0 |
3.1 |
| |
|
778.9 |
13.0 |
| |
|
867.4 |
4.2 |
| |
|
964.1 |
14.6 |
| |
|
1085.8 |
10.1 |
| |
|
1089.7 |
1.7 |
| |
|
1112.1 |
13.5 |
| |
|
1212.9 |
1.4 |
| |
|
1299.1 |
1.6 |
| |
|
1408.0 |
20.8 |
|
Now we can determine the conversion coefficient 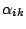 by
using the relations above, using the graphs given in appendix B.
In order to have a meaningful and correct interpretation of the extracted result an error estimation is required.
The multipolarity for the 662 keV transition can
now be determined from a diagram. When we know the multipolarity
we can deduce the spin and parity for the 662 keV level in
by
using the relations above, using the graphs given in appendix B.
In order to have a meaningful and correct interpretation of the extracted result an error estimation is required.
The multipolarity for the 662 keV transition can
now be determined from a diagram. When we know the multipolarity
we can deduce the spin and parity for the 662 keV level in 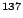 Ba
by using the selection rules.
Ba
by using the selection rules.
Try to answer the following questions before the laboration. These
questions will be the basis for a discussion
at the beginning of the lab. exercise.
- What is internal conversion?
- How is the internal conversion coefficient defined?
- What parameters does it depend on?
- What is the meaning of the multipolarity of a
electro-magnetic transition?
- What selection rules are valid for the electro-magnetic transitions?
- Why can there be no M0-transitions?
- How can a E0-transition be realised?
- How does the germanium detector work?
- What is limiting the speed of the germanium detector?
- Why is an alpha-particle stopped faster that a proton when
entering materials?
- Electrons are different from the other charged particles
when it comes to detection methods. In what way?
- What is the big advantage of the germanium
detector over the NaI detector?
- Does the NaI detector have any advantage over the germanium detector?
- What kind of statistics determine both the radioactive decay and the
detection process?
- What can be read from the so-called Bragg curve?
- What is a single-escape peak and what is
a double-escape peak?
Karin Andgren
Internal Conversion
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 internal.tex
The translation was initiated by on 2005-10-05
2005-10-05
![]() , for a charged particle slowing down in a material
is called Bethe-Blochs formula and is given by:
, for a charged particle slowing down in a material
is called Bethe-Blochs formula and is given by:
![]() is proportionated to
is proportionated to ![]() . This means for
example that an alpha particle will stop much faster
compared to a proton in a given material.
. This means for
example that an alpha particle will stop much faster
compared to a proton in a given material.
![]() photon,
but the nucleus can also interact with the electrons of its atom
to release the excess energy.
photon,
but the nucleus can also interact with the electrons of its atom
to release the excess energy.
![]() photon emitted from a nucleus will have an energy corresponding
to the difference in energy between the initial and final state of the nucleus.
The multipolarity of the photon corresponds to the angular momentum
that the photon carries away from the nucleus. If we know the
spin and parity of one of the states, we can learn something
about the spin and parity of the other state by measuring
the multipolarity of the emitted photon.
photon emitted from a nucleus will have an energy corresponding
to the difference in energy between the initial and final state of the nucleus.
The multipolarity of the photon corresponds to the angular momentum
that the photon carries away from the nucleus. If we know the
spin and parity of one of the states, we can learn something
about the spin and parity of the other state by measuring
the multipolarity of the emitted photon.

![]() m, and therefore a different
angular intensity distribution. The problem is that is is not trivial
to separate the three transitions. We can split up the levels by
applying an external magnetic field, but even a very large field
will not make it possible to separate the transitions with a
normal
m, and therefore a different
angular intensity distribution. The problem is that is is not trivial
to separate the three transitions. We can split up the levels by
applying an external magnetic field, but even a very large field
will not make it possible to separate the transitions with a
normal ![]() -ray detector. We will therefore see a sum of the
three angular distributions, and if the sub-levels are evenly
populated the sum will be isotropic. One way to solve the
problem is to lower the temperature
of the source so that the Boltzmann distribution will give an
uneven distribution of the population of the sub-levels. To
do this, the temperature must be as low as about 0.01 K.
-ray detector. We will therefore see a sum of the
three angular distributions, and if the sub-levels are evenly
populated the sum will be isotropic. One way to solve the
problem is to lower the temperature
of the source so that the Boltzmann distribution will give an
uneven distribution of the population of the sub-levels. To
do this, the temperature must be as low as about 0.01 K.
![]() radiation.
Instead, we use the fact that
the the relative intensity of internal conversion
depend on the multipolarity of the transition (the intensity
does also depend on other factors, see Krane, page 346).
By measuring the internal
conversion intensity, we can therefore deduce the multipolarity of the
transition.
radiation.
Instead, we use the fact that
the the relative intensity of internal conversion
depend on the multipolarity of the transition (the intensity
does also depend on other factors, see Krane, page 346).
By measuring the internal
conversion intensity, we can therefore deduce the multipolarity of the
transition.

![]() -ray peaks for a number of calibration sources. Using
the efficiency curve, the ratio between the detector efficiencies
for the X-rays and
-ray peaks for a number of calibration sources. Using
the efficiency curve, the ratio between the detector efficiencies
for the X-rays and ![]() -rays of interest can be measured as:
-rays of interest can be measured as:
![]() .
Diagrams that relate
.
Diagrams that relate ![]() to energy and multi-polarity can be
found in the laboratory.
From this multi-polarity we can conclude the spin and parity
for the 662 keV state of
to energy and multi-polarity can be
found in the laboratory.
From this multi-polarity we can conclude the spin and parity
for the 662 keV state of ![]() Ba by using the selection rules.
Ba by using the selection rules.
